
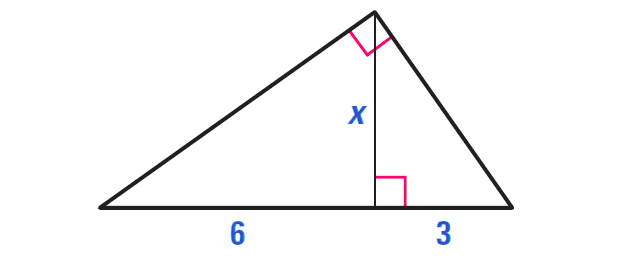
Paste the pieces back together, and you see you've filled up the squares ACEG and EFB'C'. If the altitude is drawn from the right angle of a right triangle to the hypotenuse, then the two right triangles formed are similar to the given right. Translate the triangle A'B'C' back across the square to triangle ABC, and translate the triangle AA'G across the square to the congruent triangle BB'F. Thus, what we need to show is that the square ABB'A' is equal to the sum of the squares ACEG and EFB'C'.īut that's pretty easy by cutting and pasting. Also, the square EFB'C' has side B'C' which is equal to BC, so it equals a square on the leg BC. Note that ACEG is a square on the leg AC of the original triangle. Draw a line AG to complete the square ACEG. Draw perpendiculars A'E and B'F from the points A' and B' down to the line BC. Draw a square on the hypotenuse AB, and translate the original triangle ABC along this square to get a congruent triangle A'B'C' so that its hypotenuse A'B' is the other side of the square (but the triangle A'B'C' lies inside the square). Proof: Start with the right triangle ABC with right angle at C. Here’s a nice one given by Thabit ibn-Qurra (826–901). Which statements about the two triangles must be true Select three options. Euclid’s proof is not the easiest to follow, and hundreds of others have been given. Right triangle ABC is reflected over AC, then dilated by a scale factor of to form triangle DEC. The converse says that the only triangles for which c 2 = a 2 + b 2 are right triangles in which c is the hypotenuse. You can find a very formal proof of it by Euclid, which appears in his Elements, Proposition I.47, and the converse of it in Proposition I.48. Right Triangle Similarity - Google Forms Homework by Lisa Davenport 5.0 (7) 1.75 Google Drive folder This self-grading digital assignment provides students with practice writing similarity statements for right triangles formed by the altitude and the hypotenuse of a right triangle. Square the hypotenuse and the first leg (1681 and 81), subtract the square of the first leg from the square of the hypotenuse (1600), then take the square root to get the value of the other leg b, namely 40.Īn explanation of the Pythagorean theoremĪlthough it isn’t necessary to know why the Pythagorean theorem is true, everyone has some curiosity about it. For instance, if the hypotenuse is c = 41, and one leg is a = 9, then you can determine the other leg b as follows.
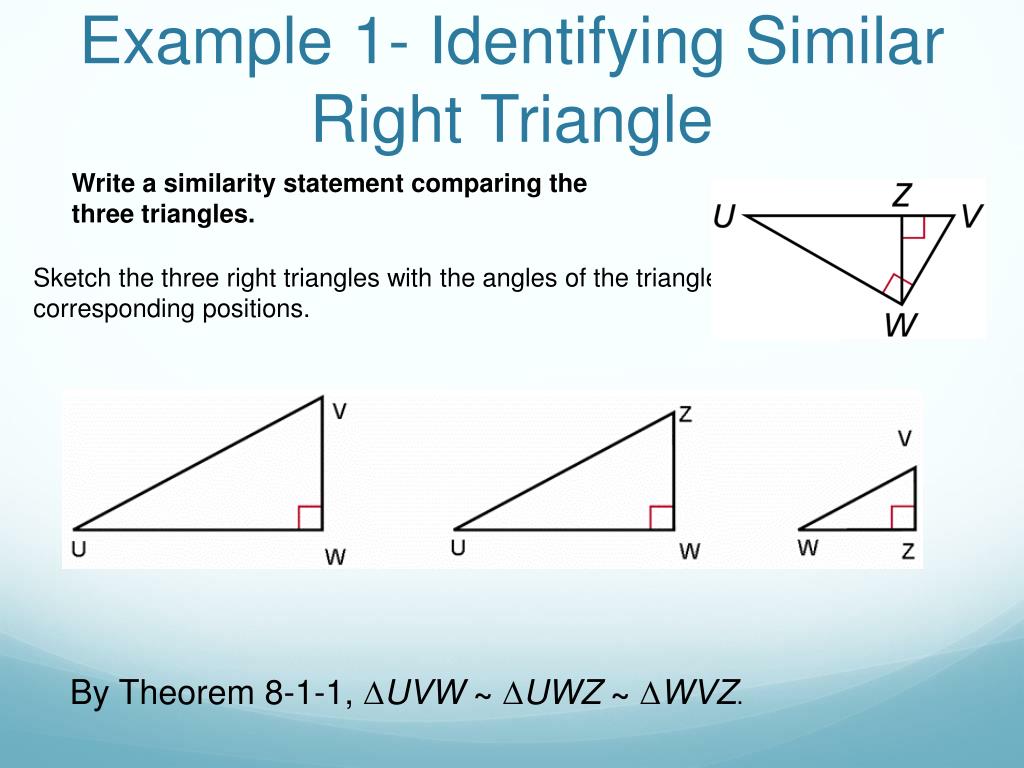
Study with Quizlet and memorize flashcards containing terms. Likewise, if you know the hypotenuse and one leg, then you can determine the other. Right Triangle Similarity Quiz QuizletThe angles in the triangles are congruent to each other. For instance, if two legs are a = 5, and b = 12, then you can determine the hypotenuse c by squaring the lengths of the two legs (25 and 144), adding the two squares together (169), then taking the square root to get the value of c, namely, 13. This theorem is useful to determine one of the three sides of a right triangle if you know the other two. The Pythagorean theorem states that the square of the hypotenuse is the sum of the squares of the other two sides, that is, The right angle be labeled C and the hypotenuse c, while A and B denote the other two angles, and a and b the sides opposite them, respectively, often called the legs of a right triangle. A right triangle is displayed in the diagram to the right.
The Pythagorean theorem is about right triangles, that is, triangles, one of whose angles is a 90° angle.


 0 kommentar(er)
0 kommentar(er)
